Large Language Models (LLMs) achieve superior performance through Chain-of-Thought (CoT) reasoning, but these token-level reasoning chains are computationally expensive and inefficient. In this paper, we introduce Compressed Latent Reasoning (CoLaR), a novel framework that dynamically compresses reasoning processes in latent space through a two-stage training approach. First, during supervised fine-tuning, CoLaR extends beyond next-token prediction by incorporating an auxiliary next compressed embedding prediction objective. This process merges embeddings of consecutive tokens using a compression factor $c$ randomly sampled from a predefined range, and trains a specialized latent head to predict distributions of subsequent compressed embeddings. Second, we enhance CoLaR through reinforcement learning (RL) that leverages the latent head's non-deterministic nature to explore diverse reasoning paths and exploit more compact ones. This approach enables CoLaR to: i) \textbf{perform reasoning at a dense latent level} (i.e., silently), substantially reducing reasoning chain length, and ii) \textbf{dynamically adjust reasoning speed} at inference time by simply prompting the desired compression factor. Extensive experiments across four mathematical reasoning datasets demonstrate that CoLaR achieves $14.1\%$ higher accuracy than latent-based baseline methods at comparable compression ratios, and reduces reasoning chain length by $53.3\%$ with only $4.8\%$ performance degradation compared to explicit CoT method. Moreover, when applied to more challenging mathematical reasoning tasks, our RL-enhanced CoLaR demonstrates performance gains of up to $5.4\%$ while dramatically reducing latent reasoning chain length by $82.8\%$.
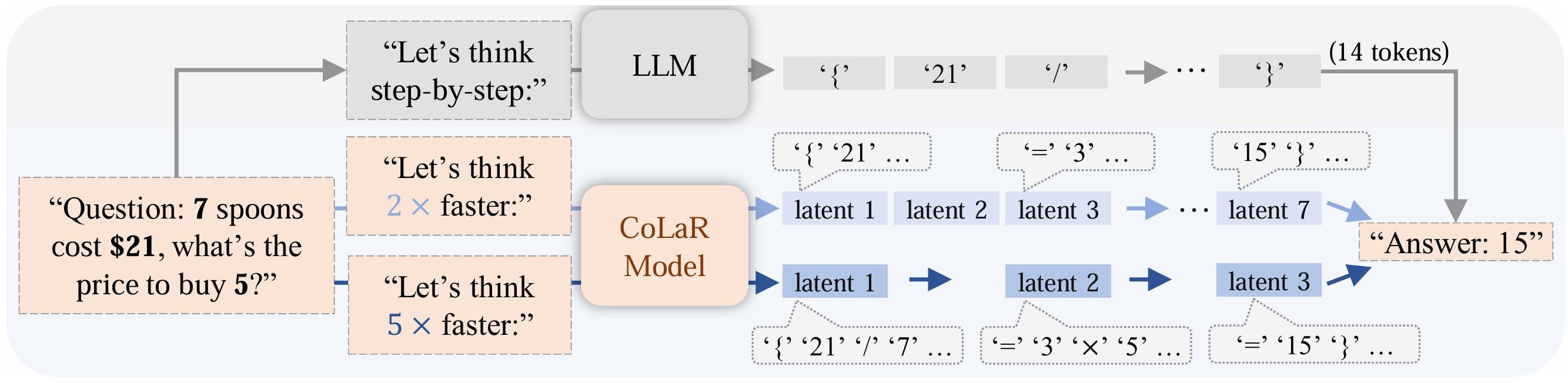
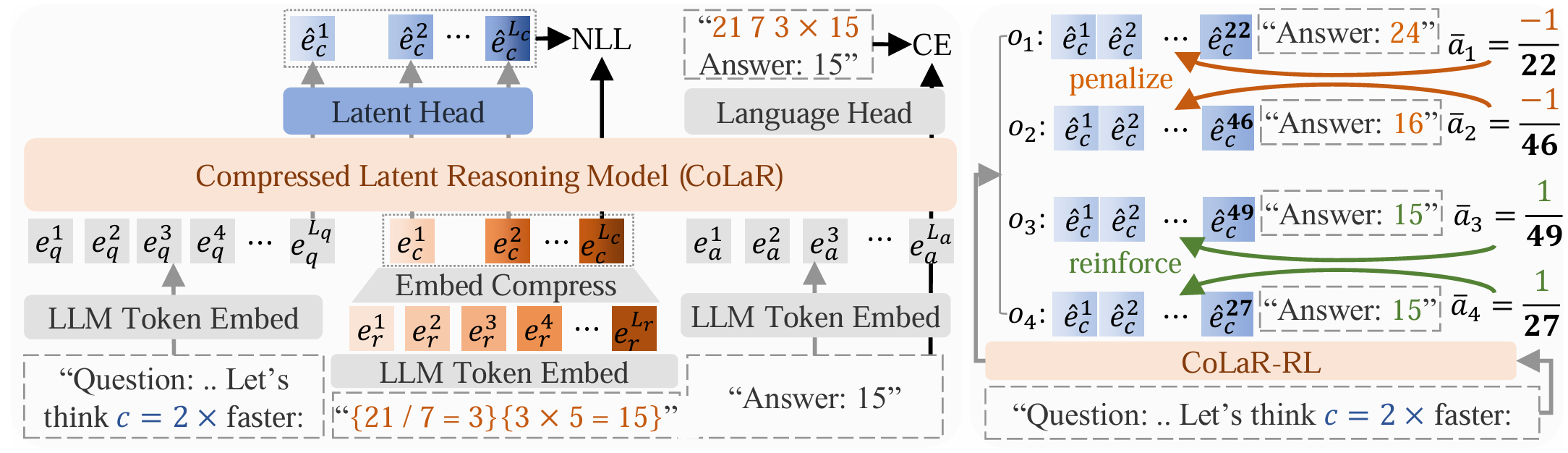
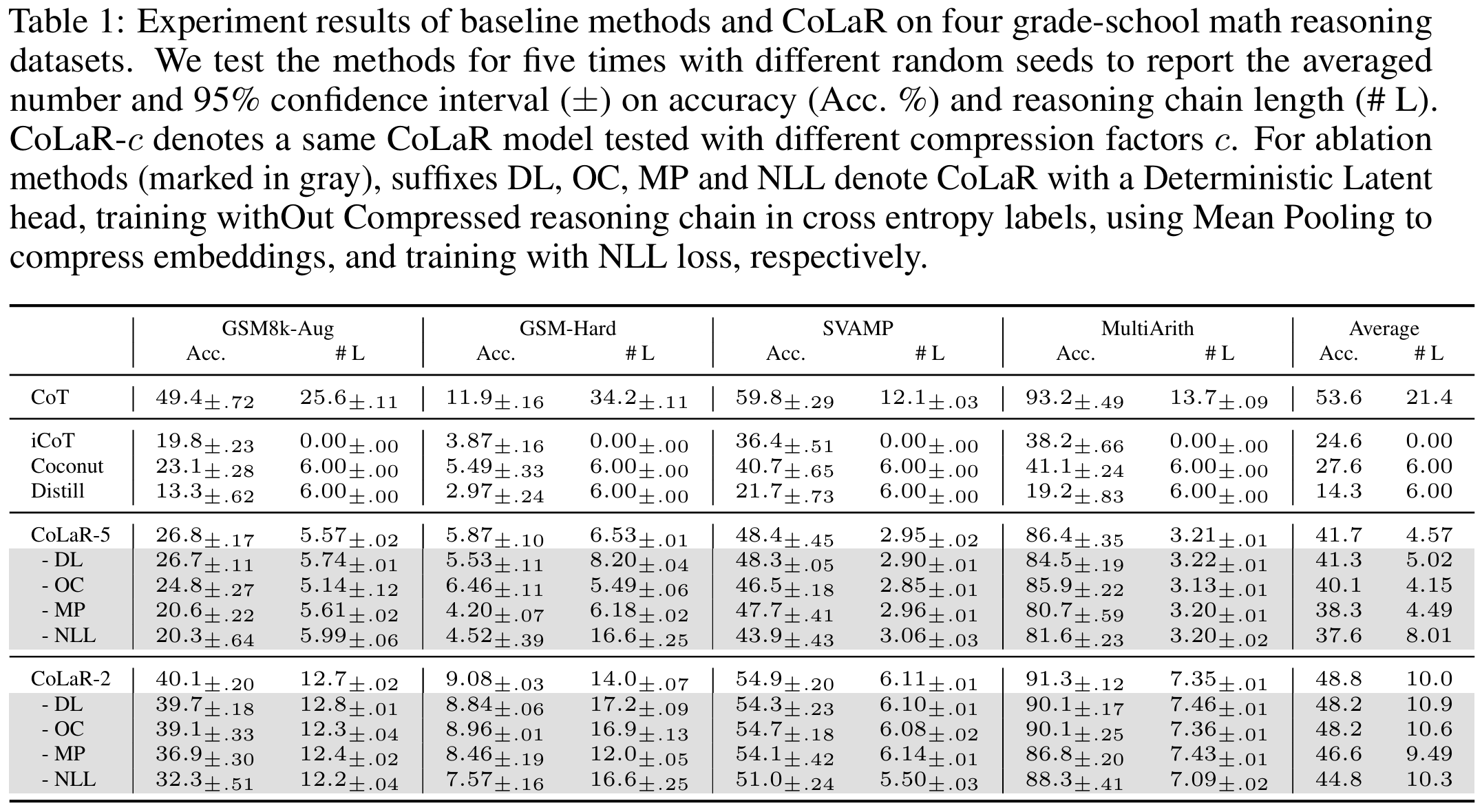
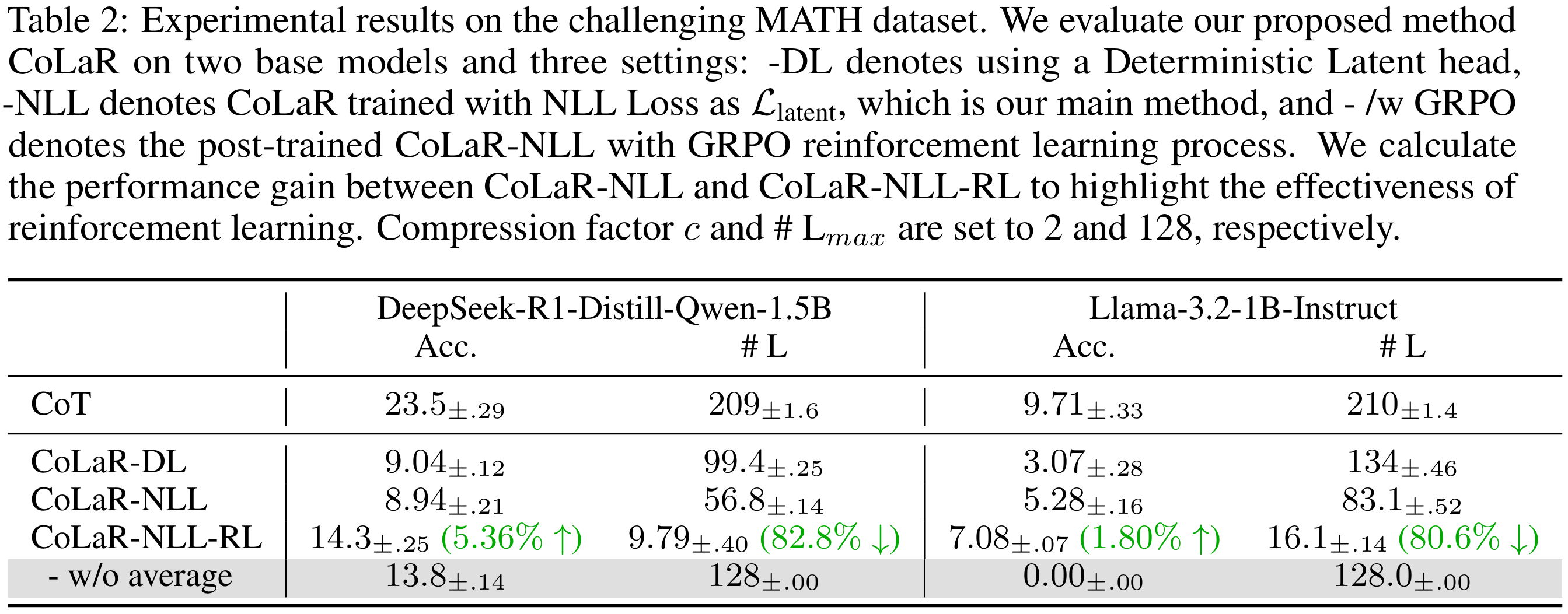
Our proposed method CoLaR consisting an LLM backbone and a Latent Head. During the \textbf{SFT stage (left)}, for each training step, CoLaR first compresses embeddings $\mathbf{e}_r$ of the original reasoning chain into compressed embeddings $\mathbf{e}_c$ with a compression factor $c$ randomly selected from the range $[1, c_{max}]$. Then, CoLaR is trained to predict: i) the compressed reasoning embeddings via the Latent Head, and ii) the compressed reasoning tokens and answer tokens through the Language Head. During the \textbf{RL stage (right)}, for every question input, CoLaR samples a group of $G$ outputs $o_{1:G}$ consisting of the latent reasoning chain and the predicted answer. We then calculate the relative rewards $a_{1:G}$ for each output, and the rewards are averaged on each token ($\bar{a}_i$), encouraging CoLaR to explore diverse latent reasoning pathways and exploit those more compact ones.
Given $\mathbf{t}, \mathbf{e}, \mathbf{h}$ denote tokens, embeddings, and hidden states, respectively, and subscripts $q, r, c, a$ denote question, reasoning chain, compressed (latent) reasoning chain, and answer, respectively,
The objective of SFT stage could be formulated as the sum of the following two losses (MathJax included):
$\mathcal{L}_{\text{comp}}=-\frac{1}{L_a+L_c}\sum_{i=1}^{L_a+L_c}\log p([\mathbf{t}_c,\mathbf{t}_a]^i|[\mathbf{e}_c, \mathbf{e}_a]^{1:i-1}, \mathbf{e}_q)$,
and
$\mathcal{L}_{\text{latent}}(i)= -\log p(e_c^i \mid \hat{\mu}_c^i, \hat{\sigma}_c^i) = \frac{(e_c^i - \hat{\mu}_c^i)^2}{2\hat{\sigma}_c^i} + \log \hat{\sigma}_c^i$.
The objective of RL stage could be formulated as:
$\mathcal{L}_{\text{GRPO}} = -\frac{1}{G}\sum_{i=1}^{G}\left( \min \left( \frac{\pi_{\theta}\left(o_i | q \right)}{\pi_{\theta_{\text{old}}}\left(o_i | q \right)}A_i, \text{clip}\left( \frac{\pi_{\theta}\left(o_i | q \right)}{\pi_{\theta_{\text{old}}}\left(o_i | q \right)}, 1 - \epsilon, 1 + \epsilon \right) A_i \right) \right)$.
In this paper, we introduce Compressed Latent Reasoning (CoLaR), a framework that dynamically compresses LLM reasoning chains into latent space while maintaining exploration-exploitation capabilities. Our method centers on three key innovations: (1) compressed latent reasoning through an auxiliary next compressed embedding prediction task that encapsulates the semantics of multiple tokens, (2) dynamic training and inference with variable compression factors that allows for flexible reasoning chain lengths and fully parallelized processing, and (3) a probabilistic latent head for reinforcement learning that enables exploration of diverse reasoning pathways for higher accuracy while exploiting shorter reasoning chains for efficiency. Our experimental results demonstrate that CoLaR achieves a $14.1\%$ improvement in accuracy compared to state-of-the-art latent-based reasoning methods, while reducing reasoning chain length by $53.3\%$ with only a $4.8\%$ performance degradation relative to explicit CoT. On the challenging MATH dataset, reinforcement learning techniques further boost CoLaR's performance by $5.36\%$ while dramatically reducing reasoning chain length by $82.8\%$. Future work will focus on addressing non-integer compression factors, exploring more sophisticated reinforcement learning approaches, and extending our dynamic compression mechanism to more diverse reasoning tasks beyond mathematics.
